Προχτές το ημερολόγιο έγραφε 8 Σεπτεμβρίου ή όπως λένε οι αμερικανοί 9/8, μια ημερομηνία που παραπέμπει στην επιτάχυνση της βαρύτητας g=9,8 m/s2. Και «εορτάζεται» ως ημέρα της βαρύτητας (όπως και η ημέρα του αριθμού π=3,14 στις 14 Μαρτίου ή 3/14).
Με μια μικρή καθυστέρηση, θα «τιμήσουμε» σήμερα την ημέρα του g με το τωρινό άρθρο.
Καταρχήν, είτε λέμε «επιτάχυνση της βαρύτητας» είτε «ένταση του πεδίου βαρύτητας» είναι το ίδιο πράγμα.
Μπορεί τα σώματα που αφήνονται ελεύθερα κοντά στην επιφάνεια της Γης να πέφτουν με επιτάχυνση 9,8 m/s2, όταν όμως ένα σώμα βρίσκεται πάνω σε ένα τραπέζι, στέκεται εκεί ακίνητο χωρίς ταχύτητα ή επιτάχυνση. Όμως «αισθάνεται» το γήινο βαρυτικό πεδίο ως την δύναμη του βάρους του, η οποία όμως εξουδετερώνεται από την δύναμη στήριξης του τραπεζιού.
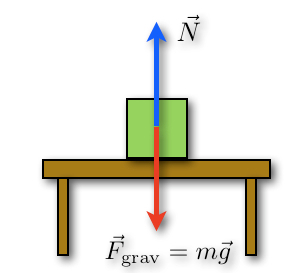
Η ένταση του πεδίου βαρύτητας σύμφωνα με την γενικότερη σχέση
ένταση πεδίου = δύναμη πεδίου / υπόθεμα
είναι
g = δύναμη του βάρους / μάζα
και κοντά στην επιφάνεια της Γης g=9,8 Ν/kg (=m/s2). Αυτή η ταύτιση επιτάχυνσης και έντασης πεδίου ισχύει μόνο για το πεδίο βαρύτητας.
Το γεγονός ότι όλα τα σώματα ανεξαρτήτως μάζας πέφτουν στο κενό με την ίδια επιτάχυνση διαπιστώθηκε για πρώτη φορά πριν από 400 χρόνια από τα πειράματα του Γαλιλαίου.
Ακόμη κι αν τα σώματα αποτελούνται από διαφορετικά υλικά πάλι πέφτουν με την ίδια επιτάχυνση.
Η συνοχή των σωμάτων γενικά διασφαλίζεται από τις ηλεκτρομαγνητικές και πυρηνικές δυνάμεις και όχι από τις βαρυτικές. Σε μια σφαίρα αλουμινίου μεγέθους μιας γροθιάς, για παράδειγμα, η ποσότητα ενέργειας που αναλώνεται στη βαρυτική έλξη μεταξύ των ατόμων του αλουμινίου, είναι μικρότερη από ένα δισεκατομμυριοστό του δισεκατομμυριοστού του δισεκατομμυριοστού της ολικής ενέργειας/μάζας της σφαίρας.
Τι συμβαίνει όμως στην υποθετική περίπτωση που τα σώματα που πέφτουν σε ένα δεδομένο βαρυτικό πεδίο έχουν τεράστια μάζα, όπως ο Ήλιος, οι πλανήτες, η Σελήνη κ.λπ. ; Πέφτουν με την ίδια επιτάχυνση;
Σε ένα σώμα όπως η Γη που περιέχει πολύ περισσότερη ύλη, η ενέργεια της βαρυτικής έλξης ή συνοχής αποτελεί ένα πολύ μεγαλύτερο κλάσμα, μόλις μικρότερη από το ένα δισεκατομμυριοστό της ενέργειας/μάζας της.
Εργαστηριακά πειράματα απέδειξαν ότι η πυρηνική και ηλεκτρομαγνητική συνεισφορά στην ενέργεια των σωμάτων αποκρίνονται όλες με τον ίδιο τρόπο σε ένα εξωτερικό βαρυτικό πεδίο, αφού σώματα διαφορετικής σύστασης ή δομής πέφτουν πάντοτε με την ίδια επιτάχυνση, ανεξαρτήτως από το εάν ένα σώμα περιέχει σχετικά περισσότερη ηλεκτρομαγνητική ενέργεια ανά μονάδα μάζας από το άλλο.
Στην πραγματικότητα αυτή ακριβώς η καθολικότητα ή ανεξαρτησία της βαρυτικής επιτάχυνσης από τη φύση του σώματος μας επέτρεψε να ερμηνεύσουμε τη βαρύτητα ως εκδήλωση της καμπύλωσης του χωροχρόνου μάλλον, παρά ως φαινόμενο που συνδέεται με συγκεκριμένα αντικείμενα.
Αλλά τι γίνεται με την ίδια τη βαρύτητα;
Δεν είναι άραγε δυνατό, λόγω κάποιας (ενδεχόμενης) μη γραμμικής αλληλεπίδρασης βαρύτητας με βαρύτητα, μεταξύ του εξωτερικού και του εσωτερικού βαρυτικού πεδίου, ένα σώμα που διαθέτει ισχυρή συνοχή μέσω βαρύτητας, να πέφτει με διαφορετική ταχύτητα μέσα σε ένα εξωτερικό πεδίο, από ένα σώμα που έχει λιγότερη ισχυρή συνοχή;
Ένας λευκός νάνος, για παράδειγμα, έχει την ίδια μάζα με τον Ήλιο, διάμετρο μόλις μερικών χιλιάδων χιλιομέτρων, ενώ η διάμετρος του Ήλιου είναι 1.400.000 χιλιόμετρα. Επειδή έχει γίνει τόσο συμπαγές λόγω της βαρύτητας, η βαρυτική ενέργεια συνοχής του είναι περίπου 1.000 φορές μεγαλύτερη από εκείνη του Ήλιου.
Αν κάποιος έριχνε έναν λευκό νάνο και τον Ήλιο δίπλα – δίπλα μέσα σε κάποιο εξωτερικό βαρυτικό πεδίο, θα έπεφταν άραγε με την ίδια επιτάχυνση;
Στο ερώτημα αυτό προσπάθησε να απαντήσει ο Kenneth Nordtvedt προς το τέλος της δεκαετίας του 1960.
Ο Nordtvedt επινόησε μια μέθοδο για να περιγράψει την κίνηση σωμάτων μεγέθους ενός πλανήτη, η οποία θα ίσχυε για οποιαδήποτε θεωρία βαρύτητας βασισμένη στην καμπύλωση του χωροχρόνου, ή τουλάχιστον σε μια μεγάλη κατηγορία τέτοιων θεωριών.
Οι εξισώσεις στις οποίες κατέληξε μπορούσαν να συμπεριλάβουν με έναν σμπάρο, τη γενική σχετικότητα, τη θεωρία Brans – Dicke και πολλές άλλες. Για να βρει κανείς την πρόβλεψη μιας συγκεκριμένης θεωρίας, όπως η γενική σχετικότητα, δεν είχε παρά να εξειδικεύσει τις εξισώσεις, διαλέγοντας συγκεκριμένες αριθμητικές τιμές κάποιων συντελεστών που εμφανίζονται σε αυτές.
Οι υπολογισμοί ήταν πολύπλοκοι και η τελική εξίσωση περιείχε πάρα πολλούς όρους, οι οποίοι περιέγραφαν την επιτάχυνση ενός σώματος μεγάλης μάζας, αλλά στο τέλος προέκυπταν δυο σημαντικά αποτελέσματα.
Πρώτον, όταν οι εξισώσεις εξειδικεύονταν για την περίπτωση της γενικής σχετικότητας, τεράστιος αριθμός όρων αλληλοαναιρείτο, με αποτέλεσμα διαφορετικά σώματα μεγάλης μάζας να εμφανίζουν ακριβώς την ίδια επιτάχυνση, ανεξαρτήτως από το πόσο ισχυρή είναι η συνολική δύναμή τους.
Επομένως, η γενική σχετικότητα προβλέπει ότι η επιτάχυνση σωμάτων με βαρυτική συνοχή είναι ίδια με την επιτάχυνση σωμάτων εργαστηριακής κλίμακας.
Με άλλα λόγια αν ρίχναμε τη Γη και μια σφαίρα αλουμινίου μέσα σε στο βαρυτικό πεδίο κάποιου μακρινού σώματος (διατηρώντας τη σφαίρα μακριά από τη Γη, τόσο όσο να μη χρειάζεται να λάβουμε υπ’ όψη την αμοιβαία βαρυτική τους έλξη), θα έπεφταν και οι δυο με την ίδια ταχύτητα.
Πρόκειται για μια αληθινά αστρονομική εκδοχή της επίδειξης του Γαλιλαίου στον κεκλιμένο πύργο της Πίζας.
Αυτή η όμορφη πρόβλεψη της γενικής σχετικότητας, η ισοδυναμία των επιταχύνσεων των σωμάτων, από τα μικρότερα ως τα μεγαλύτερα σε μέγεθος, ονομάζεται μερικές φορές ισχυρή αρχή της ισοδυναμίας.
Υπήρχε και άλλο αξιοσημείωτο αποτέλεσμα των υπολογισμών του Nordtvedt . Στις περισσότερες από τις άλλες θεωρίες της βαρύτητας, συμπεριλαμβανομένης και της θεωρίας Brans-Dicke, δεν υπήρχε πλήρης αλληλοαναίρεση των όρων, και έτσι παρέμενε μια μικρή διαφορά στις επιταχύνσεις (φαινόμενο Nordtvedt), ανάλογα με το πόσο ισχυρά συνείχε τα σώματα η ίδια τους η βαρύτητα.
Έτσι λοιπόν, μολονότι οι θεωρίες αυτές εγγυόντουσαν πως τα εργαστηριακά σώματα πέφτουν με την ίδια επιτάχυνση, αν μελετούσε κανείς σώματα με μεγάλες ποσότητες βαρυτικής αυτοσυνοχής, θα εύρισκε ότι τα σώματα αυτά θα έπεφταν με διαφορετική επιτάχυνση.
Με άλλα λόγια, στις θεωρίες αυτές η βαρυτική ενέργεια πέφτει με ελαφρώς διαφορετική ταχύτητα από τις άλλες μορφές ενέργειας όπως είναι π.χ. οι ενέργεια που αντιστοιχεί στη μάζα ηρεμίας, η ηλεκτρομαγνητική ενέργεια κ.λπ.
Οι θεωρίες όπως αυτή των Brans-Dicke ήταν λοιπόν συμβατές με τη συνηθισμένη αρχή της ισοδυναμίας αλλά όχι με την ισχυρή αρχή της ισοδυναμίας – η οποία αποτελεί ιδιότητα της γενικής σχετικότητας.
Tο φαινόμενο Nordtvedt ερευνήθηκε και πειραματικά και αποδείχθηκε πως δεν ισχύει.
Tο πώς έγινε αυτό, με την τοποθέτηση των οπισθοκλαστικών κατόπτρων στην επιφάνεια της Σελήνης από τις αποστολές Apollo, θα περιγραφεί σε μια άλλη ανάρτηση …
ΠΗΓΗ: «Είχε δίκιο ο Αϊνστάϊν;», Clifford M. Will, Πανεπιστημιακές Εκδόσεις Κρήτης
https://physicsgg.me/2013/09/10/%ce%b5%ce%bb%ce%b5%cf%8d%ce%b8%ce%b5%cf%81%ce%b7-%cf%80%cf%84%cf%8e%cf%83%ce%b7-%ce%ac%cf%83%cf%84%cf%81%cf%89%ce%bd-%ce%ba%ce%b1%ce%b9-%cf%80%ce%bb%ce%b1%ce%bd%ce%b7%cf%84%cf%8e%ce%bd/
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Το blog TEO O ΜΑΣΤΟΡΑΣ ουδεμία ευθύνη εκ του νόμου φέρει σχετικά σε άρθρα που αναδημοσιεύονται από διάφορα ιστολόγια. Δημοσιεύονται όλα για την δική σας ενημέρωση.