Το κύκλωμα που βλέπουμε στο παρακάτω διάγραμμα περιέχει τέσσερις αντιστάτες: δυο από αυτούς έχουν αντίσταση R και οι άλλοι δυο αντίσταση 3R. Tα βολτόμετρα είναι πανομοιότυπα (κι όχι ιδανικά) και οι ενδείξεις τους είναι 0,5V και 3V. Το αμπερόμετρο δείχνει 6 mA. Βρείτε την ένταση του ρεύματος που διαρρέει τον κάθε αντιστάτη και την τιμή του R.

μια σύντομη λύση:
Aφού τα βολτόμετρα είναι ίδια RV= V1/IV1=V2/IV2 ή 3V/6mA =0,5V/IV2, οπότε IV2=1mA και
 RV=500Ω.
RV=500Ω. Αν εναλλάξουμε τις ενδείξεις των βολτομέτρων προκύπτει 0,5V/6mA =3V/IV2 και IV2=36mA που είναι μεγαλύτερο από το συνολικό ρεύμα στο κύκλωμα, άρα άτοπο.
Απορρίπτονται οι διατάξεις R1=R2 , R3=R4 και R1=R3 , R2=R4 γιατί τότε το βολτόμετρο V2 θα έδειχνε μηδέν (αποδεικνύεται εύκολα με επιχειρήματα συμμετρίας)..
Έστω ότι R1=3R, R2=R,R3=R, R4=3R. Τα ρεύματα στους κλάδους ΒΓ και ΗΘ πρέπει να είναι ίσα, όπως επίσης και στους κλάδους ΖΗ και ΓΔ λόγω συμμετρίας (εναλλάσσοντας τους κλάδους αυτούς το κύκλωμα είναι πανομοιότυπο). Η φορά του ρεύματος στον κλάδο ΗΓ στην περίπτωση αυτή πρέπει να είναι προς τα πάνω (αλλιώς θα οδηγηθούμε σε άτοπο).
Εφαρμόζοντας τον 1ο κανόνα του Κirchhoff παίρνουμε ΙΓΔ+ΙΒΓ=6mA (διότι ΙΓΔ=ΙΖΗ) και ΙΒΓ+1mA=ΙΓΔ, απ’ όπου ΙΓΔ=3,5Α και ΙΒΓ=2,5Α. Από τον 2ο κανόνα του Κirchhoff στον βρόχο ΓΔΘΗΓ παίρνουμε 3,5R-2,5·3R+500·1=0 και R=125Ω.
Στο ίδιο αποτέλεσμα καταλήγουμε αν επιλέξουμε την διάταξη R1=R, R2=3R, R3=3R, R4=R, με την διαφορά ότι το ηλεκτρικό ρεύμα που διαρρέει το βολτόμετρο V2 έχει φορά προς τα κάτω.
Διαβάστε επίσης την αναλυτικότερη λύση του προβλήματος από τον Γιάννη Κυριακόπουλο
ΕΔΩ:ylikonet.gr/2020/02/09
πηγή: https://aapt.scitation.org/doi/10.1119/1.5028252
… και μια εκδοχή της παραπάνω άσκησης «πιο φιλική στον μέσο μαθητή», από τον Διονύση Μάργαρη στο Υλικό Φυσικής – Χημείας:

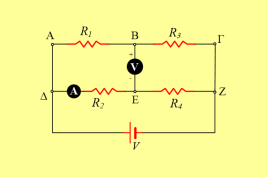
Για το κύκλωμα του διπλανού σχήματος δίνονται ότι τo βολτόμετρο με εσωτερική αντίσταση Rv=500Ω δείχνει ένδειξη Vv=VΒΕ = 50V,R1=200Ω, R2=500Ω, ενώ το ιδανικό αμπερόμετρο δείχνει ένδειξη Ι2=0,3 Α.
- Να βρεθεί η τάση VΑΒ καθώς και η ένταση Ι1 που διαρρέει τον κλάδο ΑΒ του κυκλώματος.
- Να βρεθούν οι εντάσεις των ρευμάτων που διαρρέουν τους δύο άλλους αντιστάτες και την πηγή τάσεως V.
- Αν R3=250Ω να υπολογιστούν: α) Η τιμή της αντίστασης R4. β) Η τάση V.
https://physicsgg.me/2020/02/08/%ce%b1%ce%bd%cf%84%ce%b9%cf%83%cf%84%ce%ac%cf%83%ce%b5%ce%b9%cf%82-%ce%b2%ce%bf%ce%bb%cf%84%cf%8c%ce%bc%ce%b5%cf%84%cf%81%ce%b1-%ce%ba%ce%b1%ce%b9-%ce%ad%ce%bd%ce%b1-%ce%b1%ce%bc%cf%80%ce%b5%cf%81/
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Το blog TEO O ΜΑΣΤΟΡΑΣ ουδεμία ευθύνη εκ του νόμου φέρει σχετικά σε άρθρα που αναδημοσιεύονται από διάφορα ιστολόγια. Δημοσιεύονται όλα για την δική σας ενημέρωση.