H εξίσωση Ε=mc2 που εκφράζει την ισοδυναμία μάζας – ενέργειας ανακαλύφθηκε από τον Einstein το 1905 ή ήταν γνωστή πριν από την διατύπωση της ειδικής θεωρίας της σχετικότητας; Δεν είναι και τόσο εύκολο να δοθεί μια απάντηση!
Κάποιοι αποδίδουν την εξίσωση Ε=mc2 στον Fritz Hasenöhrl, καθηγητή φυσικής στο Πανεπιστήμιο της Βιέννης. Σε μια δημοσίευσή του το 1904 ο Hasenöhrl αποδεικνύει την εξίσωση
E = 3/8 mc2
η οποία λίγο αργότερα διορθώθηκε σε
E = 3/4 mc2
Η τελευταία εξίσωση που διαφέρει από την εξίσωση της Ειδικής Σχετικότητας στον αριθμητικό παράγοντα 3/4, ήταν γνωστή από την εργασία του J. J. Thomson τo 1881 (Thomson, John Joseph (1881), “On the Electric and Magnetic Effects produced by the Motion of Electrified Bodies”).
Στενά συνδεδεμένη με ένα κινούμενο φορτίο, π.χ. ένα ηλεκτρόνιο, είναι μια ποσότητα ορμής – ακόμη και εάν το ηλεκτρόνιο δεν είχε καθόλου μάζα. Η ορμή αυτή αποδίδεται στο ηλεκτρομαγνητικό πεδίο. Χρησιμοποιώντας κλασική φυσική μπορούμε να υπολογίσουμε την ορμή του κινούμενου ηλεκτρικού φορτίου με ταχύτητα υ (βλέπε π.χ. «Διαλέξεις Φυσικής του Feynman”, τόμος Β’, σελ. 535, εκδόσεις Τζιόλα)
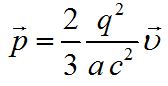
Δεδομένου ότι η ορμή ορίζεται ως το γινόμενο της μάζας επί την ταχύτητα, μπορούμε να ονομάσουμε τον συντελεστή της ταχύτητας στην παραπάνω εξίσωση ηλεκτρομαγνητική μάζα (mηλ)
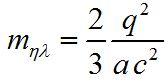
Η ενέργεια μιας επιφανειακής σφαιρικής κατανομής ηλεκτρικού φορτίου q, ακτίνας α, δίνεται από την εξίσωση
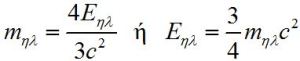
Οι Φυσικοί λοιπόν, πριν από την Ειδική Θεωρία της Σχετικότητας του Einstein, είχαν ανακαλύψει πως ένα φορτισμένο σωματίδιο μεταφέρει μια ορμή ανάλογη προς την ταχύτητά του και ότι ισχύει η εξίσωση
E = 3/4 m c2
Όταν ο Einstein και άλλοι επιστήμονες στη συνέχεια συνειδητοποίησαν ότι θα έπρεπε να ισχύει η εξίσωση Ε=mc2, στην αρχή επικράτησε μεγάλη σύγχυση μέχρι να εδραιωθεί η Θεωρία της Σχετικότητας….
Αλλά και ο Henri Poincaré το 1900 είχε φτάσει στην ακριβή εξίσωση Ε = mc2. Σύμφωνα με τα προηγούμενα η σχέση ορμής – ενέργειας για το ηλεκτρομαγνητικό πεδίο που κυκλοφορούσε ευρέως πριν την Σχετικότητα ήταν η
p = 4E/3c
αντί της ορθής
p = E/c
Όμως η τελευταία σχέση (p=E/c), αποδεικνύεται χρησιμοποιώντας κλασική φυσική χωρίς καμιά αναφορά στην έννοια των φωτονίων ή την ειδική σχετικότητα (βλέπε π.χ. σελ. 396, ΚΥΜΑΤΙΚΗ, μαθήματα φυσικής πανεπιστημίου BERKELEY, EΡΓΑΣΤΗΡΙΑ ΦΥΣΙΚΗΣ Ε.Μ.Π).
O Poincaré υπέθεσε ότι η ακτινοβολία αφού μεταφέρει ορμή θα «έχει» και μάζα m, έτσι ώστε p = mc, οπότε, δεδομένης της εξίσωσης p = E/c, προκύπτει η πιο διάσημη εξίσωση της Φυσικής Ε = mc2….
Διαβάστε επίσης: physicsworld.com – en.wikipedia.org

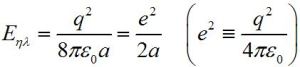
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Το blog TEO O ΜΑΣΤΟΡΑΣ ουδεμία ευθύνη εκ του νόμου φέρει σχετικά σε άρθρα που αναδημοσιεύονται από διάφορα ιστολόγια. Δημοσιεύονται όλα για την δική σας ενημέρωση.